
Bidimensional display of 31 Rational Numbers by means of the Stern-Brocot Tree [Visualisation bidimensionnelle de 31 Nombre Rationnels à l'aide de l'arbre de Stern-Brocot].

Bidimensional display of 31 Rational Numbers by means of the Stern-Brocot Tree [Visualisation bidimensionnelle de 31 Nombre Rationnels à l'aide de l'arbre de Stern-Brocot].
A+C
MedianMean(A/B,C/D) = -----
B+D
Generate(Left,Right)
{
Mean = MedianMean(Left,Right);
Generate(Left,Mean);
Generate(Mean,Right);
}
zero=0/1
infinity=1/0
Generate(zero,infinity)
level=1 0/1 > > > > > > > > > > > > > > > > > > 1/1 < < < < < < < < < < < < < < < < < < 1/0
| * | * |
| * | * |
| * | * |
| * | * |
| * | * |
| * | * |
| * | * |
| * | * |
| * | * |
level=2 0/1 > > > > > > > > 1/2 < < < < < < < < 1/1 > > > > > > > > 2/1 < < < < < < < < 1/0
| * | * | * | * |
| * | * | * | * |
| * | * | * | * |
| * | * | * | * |
level=3 0/1 > > > 1/3 < < < 1/2 > > > 2/3 < < < 1/1 > > > 3/2 < < < 2/1 > > > 3/1 < < < 1/0
| * | * * | * * | * * | * * | * * | * * | * |
| * | * * | * * | * * | * * | * * | * * | * |
(...) (...) (...) (...) (...) (...) (...) (...) (...)
 level=3 |
 level=4 |
 level=5 |
 level=6 |
 level=7 |
 level=8 |
 level=15 |
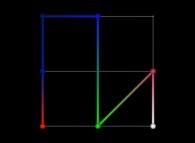 level=3 |
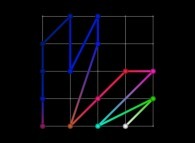 level=4 |
 level=5 |
 level=6 |
 level=7 |
 level=8 |
 |