The Liouville function displayed as a tridimensional random walk for the integer numbers from 2 to 150001 [La fonction de Liouville visualisée comme une marche aléatoire tridimensionnelle pour les nombres entiers de 2 à 150001].
The Liouville function displayed as a tridimensional random walk for the integer numbers from 2 to 150001 [La fonction de Liouville visualisée comme une marche aléatoire tridimensionnelle pour les nombres entiers de 2 à 150001].
PD(2) = 1
PD(3) = 1
PD(4) = 2
PD(5) = 1
PD(6) = 2
PD(7) = 1
PD(8) = 3
PD(9) = 2
(...)
Let's recall that 1 is not a prime number when 2 is the first one (and the only even one...).
PD(n)
L(n) = (-1)
Hence:
L(2) = -1
L(3) = -1
L(4) = +1
L(5) = -1
L(6) = +1
L(7) = -1
L(8) = -1
L(9) = +1
(...)
X(0) = 0
Y(0) = 0
Z(0) = 0
X(i+1) = X(i) + L(3*i+2)
Y(i+1) = Y(i) + L(3*i+3)
Z(i+1) = Z(i) + L(3*i+4)
(the point {X(0),Y(0),Z(0)} is at the right of the picture -white point-, when the colors used {magenta,red,yellow,green,cyan}
are an increasing function of 'i')
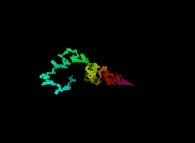with the one of a tridimensional brownian motion based on a random process 
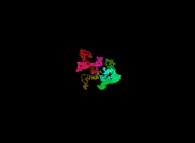and the one of a tridimensional brownian motion based on the Verhulst dynamics 
.
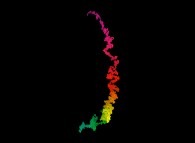where only the different prime divisors are counted.