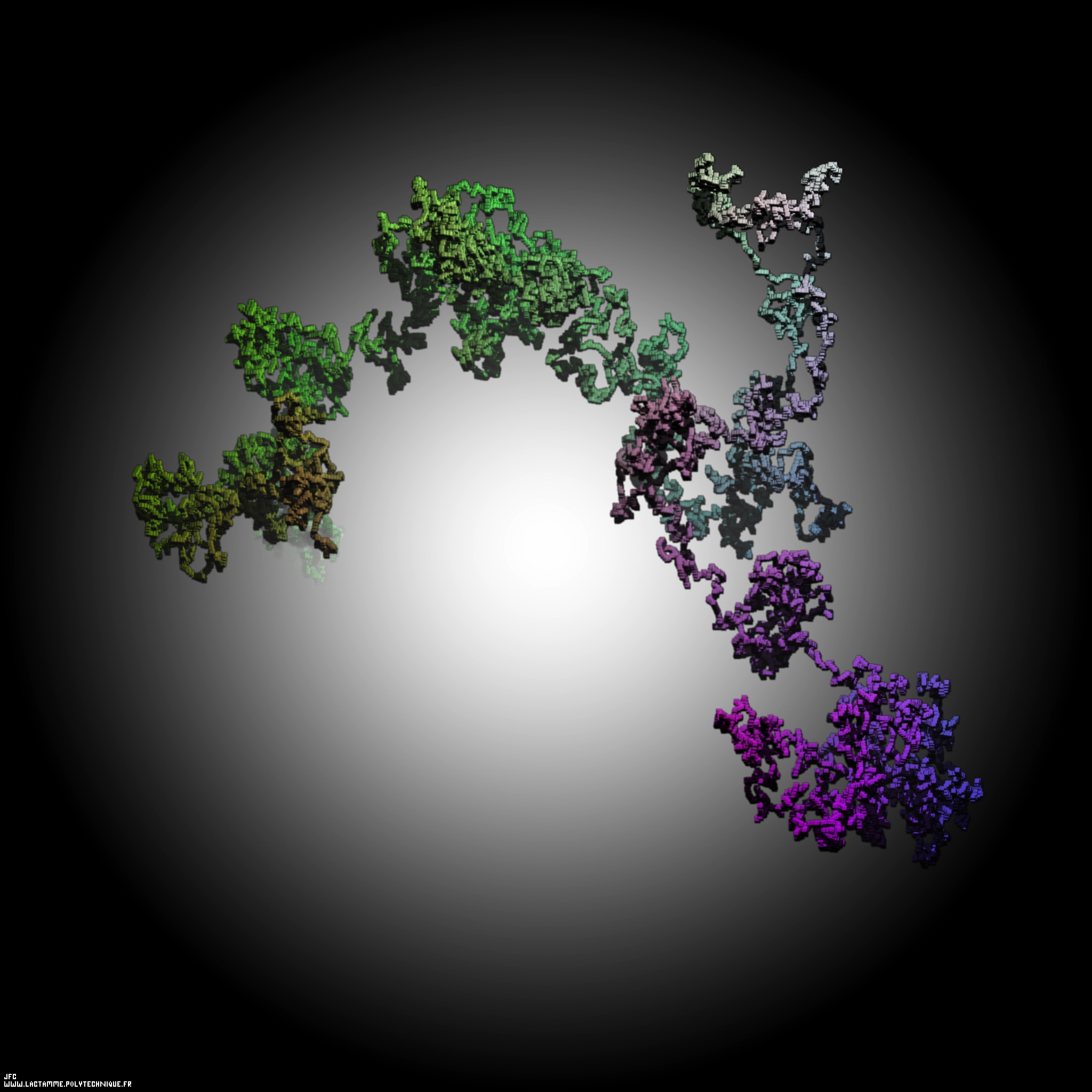
A tridimensional pseudo-random walk defined by means of 'pi': 3.141592... -20.000 digits, -base 10- with 10.000 time steps [Une pseudo-marche aléatoire tridimensionnelle définie à l'aide de 'pi': 3.141592... -20.000 chiffres, -base 10- avec 10.000 pas de temps].
The first digits of 'pi' are giving birth to two sets 'Theta' and 'Phi' using the following way:
-------> Theta = 3 4 5 2 5 5 9 9 ...
| \ / \ / \ / \ / \ / \ / \ / \ /
pi = 3.141592653589793... --> 3141592653589793... | \ / \ / \ / \ / \ / \ / \ / \ /
| \ / \ / \ / \ / \ / \ / \ / \ /
-------> Phi = 1 1 9 6 3 8 7 3
Then 'Theta' and 'Phi' are renormalized inside [0,π] and [0,(9/10).(2.π)] respectively.
Then elementary tridimensional translations {DX,DY,DZ} are defined:
DX = DR.cos(Phi).sin(Theta)
DY = DR.sin(Phi).sin(Theta)
DZ = DR.cos(theta)
(DR being an arbitrary constant) and used as the successive steps of an "absolute" tridimensional random walk..
The coordinates {X,Y,Z} are renormalized as follows:
[-0.063,+0.546]x[+0.418,+0.911]x[-0.442,+0.248] --> [0.1,0.9]x[0.1,0.9]x[0.1,0.9]
See some related pictures (possibly including this one):










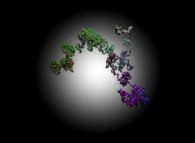





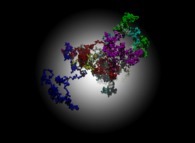
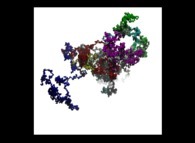
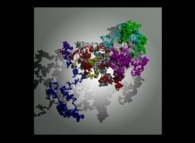
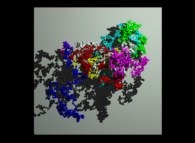
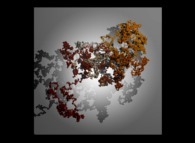

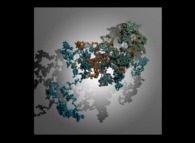
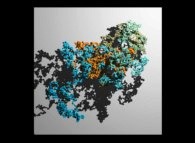







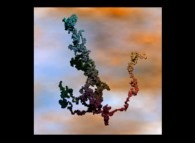
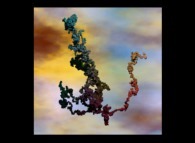

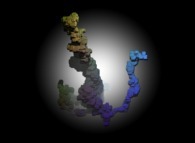
[See the 100.000 first digits -base 10- of 'pi'.]
(CMAP28 WWW site: this page was created on 06/05/2024 and last updated on 09/05/2024 14:17:19 -CEST-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Please visit the related Pi picture gallery [Visitez la galerie d'images Pi associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2024-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2024-2024.










































