The Bertrand paradox [Le paradoxe de Bertrand].
Soit un disque D dans un domaine plan E.
Des droites sont jetées au hasard dans E; seules sont conservées
celles qui intersectent D. Quelle est alors la probabilité P pour que la longueur
de la corde d'intersection soit supérieure à la longueur du côté du triangle équilateral
inscrit dans D? Suivant le modèle utilisé pour décrire le problème,
diverses réponses peuvent être obtenues: 1/2, 1/3, 1/4,...
(c'est là le paradoxe de Bertrand).
Le problème peut être généralisé en donnant à D d'une part une forme arbitraire (éventuellement
non connexe) et d'autre part une densité. Une droite aléatoire intersectant D coupe ce
dernier en deux domaines D1 et D2. Quelle est alors la probabilité P pour que le rapport
R=MASSE(D1)/MASSE(D) (ou évidemmnent R=MASSE(D2)/MASSE(D)) soit compris entre S et 1-S?
Le problème initial correspond évidemment
à un domaine D circulaire de densité uniforme avec:
___
/
4π - 3.\/ 3
S = --------------- ~ 0.1955011094778853
12π
Dans les expériences virtuelles qui seront faites, le domaine E
sera rectangulaire et limité par les bords des images représentatives,
un paramètre important étant le rapport AIRE(D)/AIRE(E).
Chacune des droites aléatoires sera définie à l'aide d'une part de l'un de ses points obtenu par
un tirage aléatoire uniforme dans E et d'autre part de l'angle qu'elle fait
fait avec l'horizontale obtenu par un tirage aléatoire uniforme dans [-π/2,+π/2].
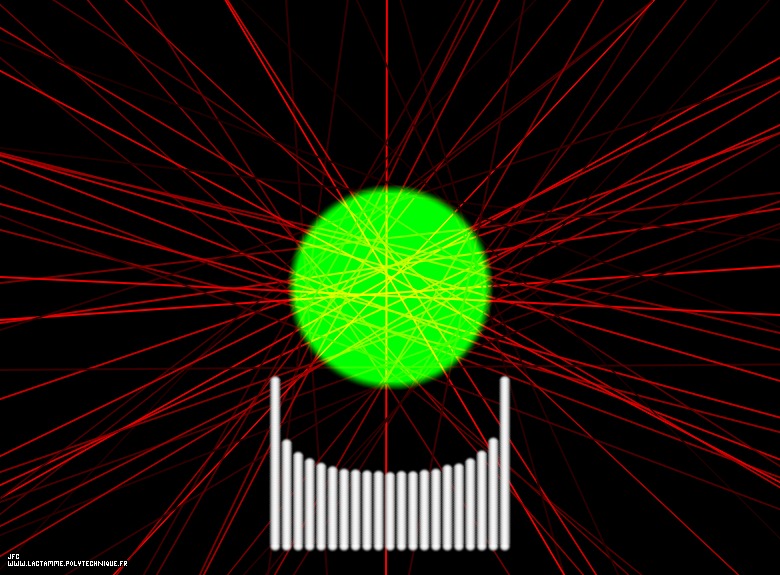
Dans l'expérience ici visualisée, le domaine D (circulaire et de densite uniforme) apparait en vert.
Le rapport AIRE(D)/AIRE(E) est égal a 30787/448500=0.0686.
1000000 droites aléatoires ont été générées, 318134 d'entre-elles intersectant D.
L'histogramme blanc montre la distribution des rapports R (dans [0,1]) de ces dernières droites.
La probabilité P mesurée ici est égale à 161744/318134=0.5084 (très voisine de 1/2).
Seules 57 droites sont visualisées (en rouge) avec une luminance proportionnelle à R si R<1/2 et
à 1-R sinon.
(CMAP28 WWW site: this page was created on 01/22/2005 and last updated on 10/06/2024 09:35:41 -CEST-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Please visit the related DeterministicChaos picture gallery [Visitez la galerie d'images DeterministicChaos associée]]
[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2005-2024.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2005-2024.

