Finally, in the year 1687, Sir Isaac Newton
published his famous Philosophiae Naturalis Principia Mathematica,
where the laws of the classical mechanics can be found.
Then, each main body of the Solar System is subject
to the following acceleration:
2 ----> i=N
d OC ----- M
k \ i ----->
--------- = / G ----------- C C
2 ----- 3 k i
dt i=1 |----->|
(i#k) | C C |
k i
By means of a numerical integration method, the preceding system of
differential equations is integrated. The trajectory of each body is then known
as a set of points:
-------> ----------> ----------> ---------->
S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
k k k k k
'dt' denoting the integration time step.
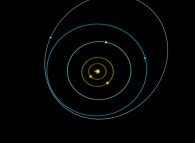
This allows us to display the motion of the 9 planets  using all the computed sets S(k) for the N=9+1 main bodies of the Solar System:
using all the computed sets S(k) for the N=9+1 main bodies of the Solar System:
/ -------> ----------> ----------> ---------->
| S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
| 1 1 1 1 1
|
| -------> ----------> ----------> ---------->
| S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
< 2 2 2 2 2
|
| (...)
|
| -------> ----------> ----------> ---------->
| S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
\ N N N N N
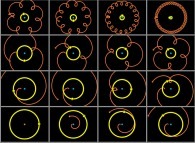
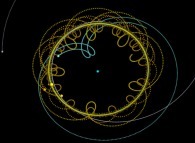
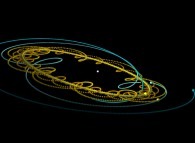
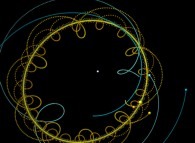
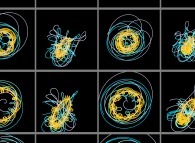
Instead of using a fixed point O (in the preceding lines, this point was in the close
neighbourhood of the Sun)
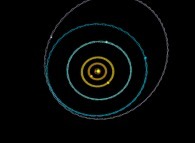
in order to visualize the trajectories, it is possible to use a moving one and in
particular, the arbitrary body number R. For the body number k, the set of points
to be visualized becomes:
-------> -------> ----------> ----------> ----------> ----------> ----------> ---------->
S' = {[ OC (0) - OC (0) ] , [ OC (1.dt) - OC (1.dt) ] , [ OC (2.dt) - OC (2.dt) ] ,..., [ OC (n.dt) - OC (n.dt) ] ,...}
k k R k R k R k R
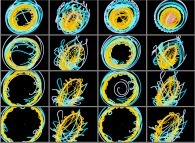
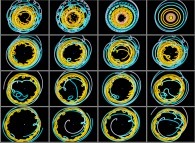
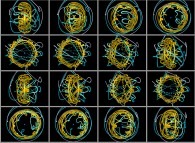
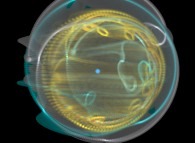
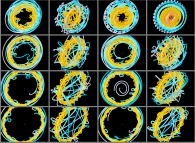
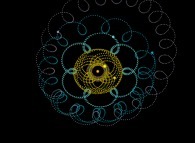
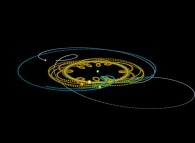
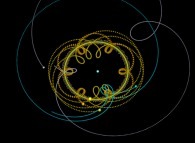
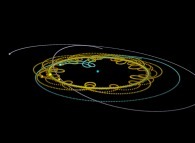
Using this simple idea will give us very new visualizations of the Solar System
as exhibited in the following lines...