Definition and Animation of Bi- and Tridimensional Manifolds
by Means of Pseudo-Projections,
Picture Self-Transformations
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 12/24/2004 and last updated on 10/03/2024 17:10:39 -CEST-)
[en français/in french]
Abstract: Tridimensional surfaces -bidimensional manifolds- can be defined by means of three matrices
and then by means of three grey scale pictures -or again one color picture-.
An arbitrary dynamics of a tridimensional surface could then be defined by means of an animation.
This can be extended to higher dimensions and used to define picture self-transformation methods.
Keywords: Holographic Principle, Pseudo-Projection, Tridimensional Surfaces, Bidimensional Manifolds, Tridimensional Manifolds, Picture Self-Transformations.
Contents of this page:
1-PICTURES:
A black and white picture is defined as a rectangular array (or again a matrix) of pixels.
Each of them contains a numerical value; the smallest and biggest possible
values represent the black and the white levels
respectively.
Most of the time these values are integer numbers between 0 and 255, but in order to improve
the computation precision real numbers (for example between -1 and +1) can be used.
A color picture can be defined as a set of three black and white pictures
each one of them corresponding to one of the primary colors (red,
green and blue respectively).
2-TRIDIMENSIONAL SURFACES (BIDIMENSIONAL MANIFOLDS):
Many surfaces -bidimensional manifolds- in a tridimensional space
can be defined using a set of three equations:
X = Fx(u,v)
Y = Fy(u,v)
Z = Fz(u,v)
with:
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
For example:
Fx(u,v) = R.sin(u).cos(v)
Fy(u,v) = R.sin(u).sin(v)
Fz(u,v) = R.cos(u)
with:
u ∈ [0,pi]
v ∈ [0,2.pi]
defines a sphere with R as the radius and the origin of the coordinates as the center.
[Umin,Umax]*[Vmin,Vmax] then defined a bidimensional rectangular domain D.
v ^
|
V |...... ---------------------------
max | |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
V |...... ---------------------------
min | : :
| : :
O------------------------------------------------->
U U u
min max
If D is sampled by means of a bidimensional rectangular grid (made of Nu*Nv points),
the three {X,Y,Z} coordinates can be defined by means of three rectangular matrices:
X = Mx(i,j)
Y = My(i,j)
Z = Mz(i,j)
with:
i = f(u,Umin,Umax,Nu)
j = g(v,Vmin,Vmax,Nv)
where 'f' and 'g' denote two obvious linear functions...
Then it is possible to define a tridimensional surface -a bidimensional manifold-
by means of three matrices.
It is noteworthy to recall that a picture is a matrix and then,
a tridimensional surface
can be defined by means of three black and white pictures
or again by means of one color picture: something like
an holographic principle. That will allow us to do with the
surfaces all that can be done with the pictures (filterings, deformations,
interpolations, arithmetic operations,...).
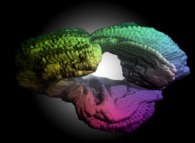
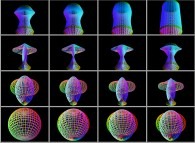
Let's give a deeper understanding of this process using the case of the sphere. Here are the three matrices
Mx, My and Mz:
- Mx(i,j) =
 = Fx(u,v) = sin(u).cos(v)
= Fx(u,v) = sin(u).cos(v)
- My(i,j) =
 = Fy(u,v) = sin(u).sin(v)
= Fy(u,v) = sin(u).sin(v)
- Mz(i,j) =
 = Fz(u,v) = cos(u)
= Fz(u,v) = cos(u)
The "additive" superposition (red+green+blue)
of these three matrices (black and white pictures) gives the following color picture:
 +
+  +
+  =
= 
that is the color picture associated to the sphere (its pseudo-projection).
The respective levels of red,
green and blue of the point {i,j} give the tridimensional coordinates
{Fx(u,v),Fy(u,v),Fz(u,v)} of one of the point of this sphere.
Obviously, the three matrices are defining only a limited set of points.
The other points are obtained by means of interpolations using defined neighbours
:
-
 ==
== 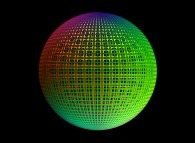 a sphere.
a sphere.
-
 ==
== 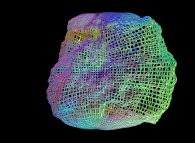 a crumpled sphere (some fractal "noise" added on the {X,Y,Z} coordinates).
a crumpled sphere (some fractal "noise" added on the {X,Y,Z} coordinates).
-
 ==
==  a crumpled sphere (some fractal "noise" added on the radius coordinate).
a crumpled sphere (some fractal "noise" added on the radius coordinate).
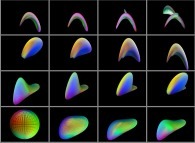
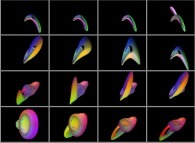
The surface colors are obviously arbitrary. But for all examples here provided, the
gradients of the three functions Fx, Fy and Fz are locally defining the
three Red, Green and Blue components.
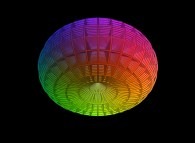
Here are some numerous examples:
-
 ==
==  a plane.
a plane.
-
 ==
== 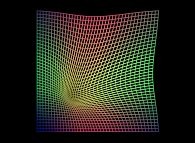 a distorted plane.
a distorted plane.
-
 ==
== 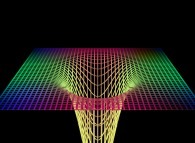 a "pseudo-gaussian plane".
a "pseudo-gaussian plane".
-
 ==
== 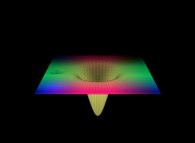 a "pseudo-bi-gaussian plane".
a "pseudo-bi-gaussian plane".
-
 ==
== 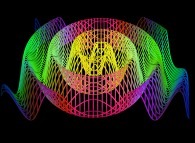 a "spiraling plane".
a "spiraling plane".
-
 ==
==  a Peano "fractal plane".
a Peano "fractal plane".
-
 ==
==  a "fractal plane" with overhangings.
a "fractal plane" with overhangings.
-
 ==
==  a "fractal plane" with overhangings.
a "fractal plane" with overhangings.
-
 ==
== 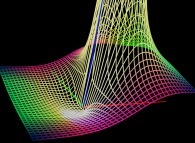 the relief -modulus- of the function exp(1/z).
the relief -modulus- of the function exp(1/z).
-
 ==
== 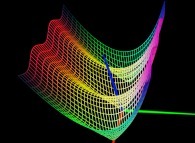 the relief -modulus- of the function sin(z).
the relief -modulus- of the function sin(z).
-
 ==
==  a crumpled cylinder (some fractal "noise" added).
a crumpled cylinder (some fractal "noise" added).
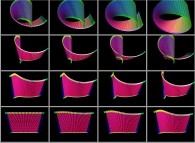
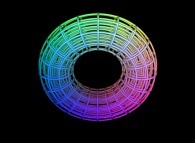
-
 ==
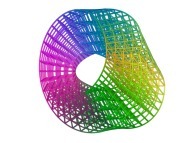
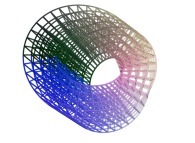
== 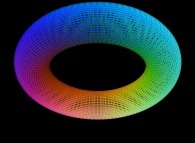 a torus.
a torus.
-
 ==
==  a crumpled torus (some fractal "noise" added).
a crumpled torus (some fractal "noise" added).
-
 ==
==  a crumpled torus (some fractal "noise" added).
a crumpled torus (some fractal "noise" added).
-
 ==
==  the second 'power' of a torus.
the second 'power' of a torus.
-
 ==
==  the third 'power' of a torus.
the third 'power' of a torus.
-
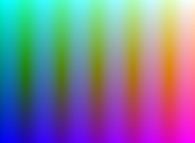 ==
==  the modulus of the complex sine function.
the modulus of the complex sine function.
-
 ==
== 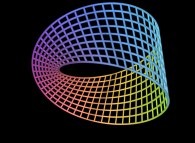 the Möbius strip.
the Möbius strip.
-
 ==
==  the Klein bottle.
the Klein bottle.
-
 ==
==  the Klein bottle (the coloring is made using the
pseudo-projection itself).
the Klein bottle (the coloring is made using the
pseudo-projection itself).
-
 ==
== 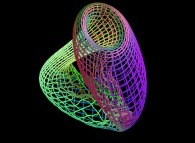 a crumpled Klein bottle (some fractal "noise" added).
a crumpled Klein bottle (some fractal "noise" added).
-
 ==
== 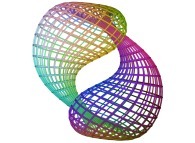 the double Jeener bottle.
the double Jeener bottle.
-
 ==
== 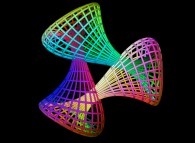 the Jeener's triple Klein bottle.
the Jeener's triple Klein bottle.
-
 ==
== 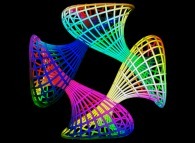 the Jeener's quadruple bilateral bottle.
the Jeener's quadruple bilateral bottle.
-
 ==
== 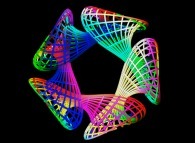 the Jeener's quintuple Klein bottle.
the Jeener's quintuple Klein bottle.
-
 ==
== 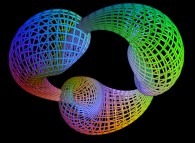 the Bonan-Jeener's triple Klein bottle.
the Bonan-Jeener's triple Klein bottle.
-
 ==
==  a shell (Jeener surface 1).
a shell (Jeener surface 1).
-
 ==
==  a 'crumpled' Jeener 'bulot'.
a 'crumpled' Jeener 'bulot'.
-
 ==
==  a 'crumpled' Jeener 'bulot'.
a 'crumpled' Jeener 'bulot'.
-
 ==
== 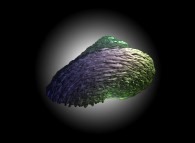 a 'crumpled' Jeener 'bulot'.
a 'crumpled' Jeener 'bulot'.
-
 ==
==  the Boy surface.
the Boy surface.
-
 ==
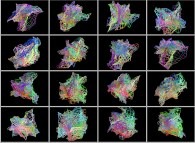
== 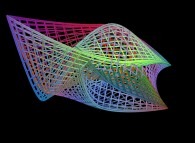 a fractal surface (two iterations).
a fractal surface (two iterations).
-
 ==
== 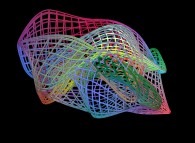 a fractal surface (three iterations).
a fractal surface (three iterations).
-
 ==
== 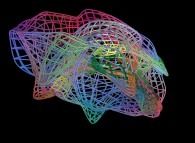 a fractal surface (four iterations).
a fractal surface (four iterations).
-
 ==
==  a fractal surface (five iterations).
a fractal surface (five iterations).
-
 ==
== 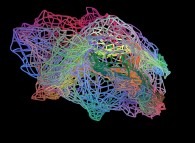 a fractal surface (six iterations).
a fractal surface (six iterations).
-
 ==
== 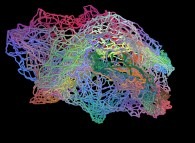 a fractal surface (numerous iterations...).
a fractal surface (numerous iterations...).
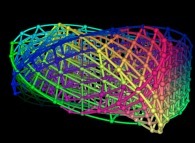
3-COMBINATION AND MIXING OF TRIDIMENSIONAL SURFACES (BIDIMENSIONAL MANIFOLDS):
It is easy to combine and mix surfaces by means of their associated color pictures.
Here are some examples:
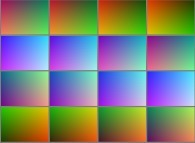
4-ANIMATION OF TRIDIMENSIONAL SURFACES (BIDIMENSIONAL MANIFOLDS):
Thus, a tridimensional surface can be defined by means of one color picture.
An arbitrary dynamics of a tridimensional surface could then be defined using a
set of color pictures or again a color animation.
Here are some examples:
At last, it is obvious that
a set of tridimensional surfaces could be defined using
the juxtaposition of color pictures or again
a set of color pictures -ie. a color animation-.
Here are some examples:
Holes and distorsions of the 'u' and 'v' coordinates can be added as on these examples:
-
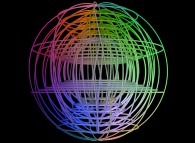 a set of twisted spheres.
a set of twisted spheres.
-
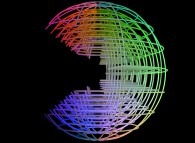 a set of spheres with holes.
a set of spheres with holes.
At last, this process facilitates the interpolation between surfaces as on this example:
-
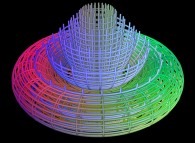 from a torus to a cylinder.
from a torus to a cylinder.
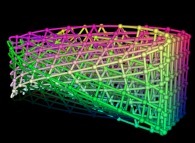
5-TRIDIMENSIONAL MANIFOLDS:
This can be extended to tridimensional manifolds. Thus:
Many tridimensional manifolds in a tridimensional space
can be defined using a set of three equations:
X = Fx(u,v,w)
Y = Fy(u,v,w)
Z = Fz(u,v,w)
with:
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
w ∈ [Wmin,Wmax]
[Umin,Umax]*[Vmin,Vmax]*[Wmin,Wmax] then defined a tridimensional rectangular domain D.
If D is sampled by means of a tridimensional rectangular grid (made of Nu*Nv*Nw points),
the three {X,Y,Z} coordinates can be defined by means of a set of Nw rectangular matrice triplets:
X = {Mxk(i,j)}
Y = {Myk(i,j)}
Z = {Mzk(i,j)}
with:
i = f(u,Umin,Umax,Nu)
j = g(v,Vmin,Vmax,Nv)
k = g(w,Wmin,Wmax,Nw)
where 'f', 'g' and 'h' denote two obvious linear functions...
Then it is possible to define a tridimensional manifold by means
of a set of Nw matrice triplets.
It is noteworthy to recall that an animation is a set of N color pictures and then,
a tridimensional manifold
can be defined by means of one (arbitrary) color animation...
Here are some examples:
6-PICTURE SELF-TRANSFORMATIONS:
Then, any color picture can be used to define a surface. Moreover,
this picture (seen as a texture) can be mapped on its associated surface (using the {u,v} coordinates
as the cartesian texture coordinates).
It is suggested to symmetrize this texture in order to avoid discontinuities
in the case of closed surfaces.
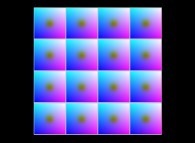
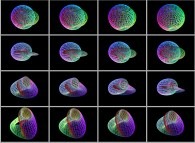
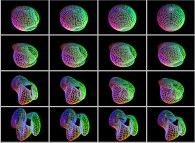
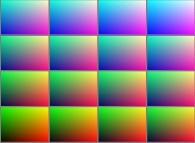
For example, the sphere  is defined
with the following picture
is defined
with the following picture  as described earlier. After its symmetrization, it gives birth
to the so-called canonical texture of the sphere:
as described earlier. After its symmetrization, it gives birth
to the so-called canonical texture of the sphere:  .
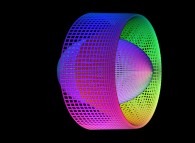
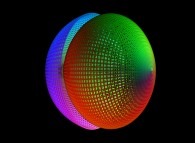
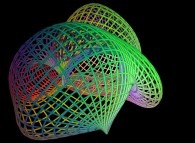
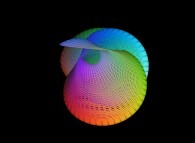
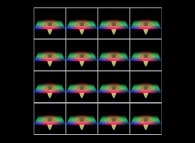
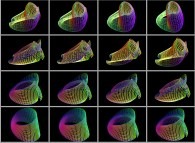
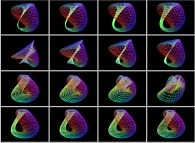
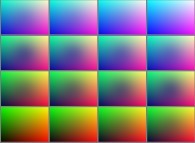
This texture picture is distorted during the mapping;
this process is the so-called self-transformation
of the initial picture:
.
This texture picture is distorted during the mapping;
this process is the so-called self-transformation
of the initial picture:  .
.
Here is the used process:
X = Fx(u,v)
Y = Fy(u,v)
Z = Fz(u,v)
The tridimensional coordinates {X,Y,Z} are then projected:
Xp= ProjectionX(X,Y,Z)
Yp= ProjectionY(X,Y,Z)
The distorsion is the defined as:
DISTORSION(u,v) = TEXTURE(Xp,Yp )
'TEXTURE' being the picture "texture" to be self-transformed.
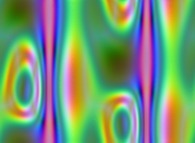
Here are some examples of picture self-transformations without displaying the associated surfaces:
-
 =>
=> 
-
 =>
=> 
-
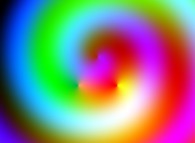 =>
=> 
-
 =>
=> 
-
 =>
=> 
-
 =>
=> 
-
 =>
=>  (in this example, a Fourier filtering was applied to the initial picture in order to smooth it
).
(in this example, a Fourier filtering was applied to the initial picture in order to smooth it
).
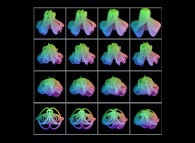
This process can be applied to color animations thus giving birth to complex texture animations.
Here are some examples:
Copyright © Jean-François COLONNA, 2004-2024.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2004-2024.




 +
+  +
+  =
= 





















































































































































































 .
This texture picture is distorted during the mapping;
this process is the so-called self-transformation
of the initial picture:
.
This texture picture is distorted during the mapping;
this process is the so-called self-transformation
of the initial picture:  .
.













