LA CONJECTURE DE GOLDBACH :
Tout nombre pair strictement supérieur à 2 serait, d'au moins une façon,
la somme de deux nombres premiers :
4 = 2+2
6 = 3+3
8 = 3+5 [= 5+3]
10 = 3+7 = 5+5 [= 7+3]
(...)
990 = 7+983 = 13+977 = 19+971 = 23+967 = 37+953 = 43+947 = 53+937 = 61+929 = 71+919 = 79+911
= 83+907 = 103+887 = 107+883 = 109+881 = 113+877 = 127+863 = 131+859 = 137+853 = 151+839 = 163+827
= 167+823 = 179+811 = 181+809 = 193+797 = 229+761 = 233+757 = 239+751 = 251+739 = 257+733 = 263+727
= 271+719 = 281+709 = 307+683 = 313+677 = 317+673 = 331+659 = 337+653 = 347+643 = 349+641 = 359+631
= 373+617 = 383+607 = 389+601 = 397+593 = 419+571 = 421+569 = 433+557 = 443+547 = 449+541 = 467+523
= 487+503 = 491+499
[= 499+491 = 503+487 = 523+467 = 541+449 = 547+443 = 557+433 = 569+421 = 571+419 = 593+397 = 601+389
= 607+383 = 617+373 = 631+359 = 641+349 = 643+347 = 653+337 = 659+331 = 673+317 = 677+313 = 683+307
= 709+281 = 719+271 = 727+263 = 733+257 = 739+251 = 751+239 = 757+233 = 761+229 = 797+193 = 809+181
= 811+179 = 823+167 = 827+163 = 839+151 = 853+137 = 859+131 = 863+127 = 877+113 = 881+109 = 883+107
= 887+103 = 907+83 = 911+79 = 919+71 = 929+61 = 937+53 = 947+43 = 953+37 = 967+23 = 971+19
= 977+13 = 983+7]
(...)
Nota : 990 est le nombre pair inférieur à 1000 possédant le plus de décompositions (104).
Contrairement aux conjectures de Syracuse
et des nombres premiers jumeaux,
en ce qui concerne celle de Goldbach
ou encore celle de Legendre,
l'ordinateur pourrait permettre de trouver un contre-exemple (c'est-à-dire un nombre pair
non décomposable additivement). Mais s'il en existe un, la probabilité pour qu'il nous soit accessible est
quasiment nulle (en fait tous les nombres entiers sont énormes voire inimaginables,
sauf évidemment les premiers : ceux que l'on utilise dans la vie courante...).
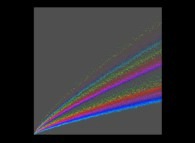
Le nombre d de décompositions possibles d'un entier donné n
est une fonction "statistiquement croissante" d=f(n) a priori inconnue.
Cette dernière peut prendre a priori n'importe quelle valeur entre 1 et n/(2*log(n))
[voir le théorème d'Hadamard et de la Vallée Poussin relatif à la densité des nombres premiers].
Alors si 1, 2, 3,...
sont des valeurs possibles, pourquoi 0 ne le serait pas aussi (et si tel était le cas,
cela invaliderait la conjecture de Legendre...) ?
Il semble que la situation serait "plus simple" si f(n) n'avait qu'une valeur possible : 1, mais de toute évidence ce n'est pas le cas...
LA CONJECTURE DE GOLDBACH :
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 21/04/2020 et mise à jour le 22/10/2025 13:29:03 -CEST-)
Copyright © Jean-François COLONNA, 2020-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2020-2025.