Enfin (provisoirement...), en l'an 1687, Sir Isaac Newton
publia les fameux Philosophiae Naturalis Principia Mathematica,
où les lois de la mécanique classique firent leur apparition.
Ainsi, chacun des N corps principaux du système solaire est soumis à
l'accélération suivante :
2 ----> i=N
d OC ----- M
k \ i ----->
--------- = / G ----------- C C
2 ----- 3 k i
dt i=1 |----->|
(i#k) | C C |
k i
A l'aide d'une méthode d'intégration numérique, le système
d'équations différentielles précédent peut être intégré. La trajectoire de chacun
des corps est alors connue par un ensemble de points qui l'échantillonnent :
-------> ----------> ----------> ---------->
S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
k k k k k
'dt' représentant le pas de temps d'intégration.
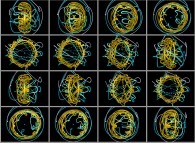
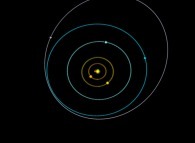
Cela nous permet donc de visualiser
le mouvement des 9 planètes 
en utilisant tous les ensembles S(k) calculés pour les N=9+1 corps principaux
du système solaire :
/ -------> ----------> ----------> ---------->
| S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
| 1 1 1 1 1
|
| -------> ----------> ----------> ---------->
| S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
< 2 2 2 2 2
|
| (...)
|
| -------> ----------> ----------> ---------->
| S = { OC (0) , OC (1.dt) , OC (2.dt) ,..., OC (n.dt) ,...}
\ N N N N N
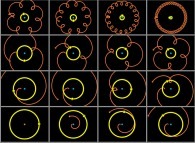
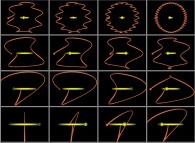
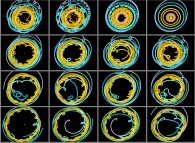
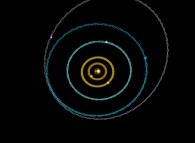
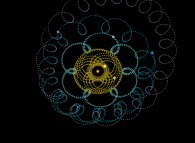
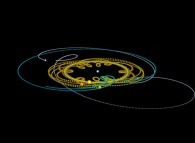
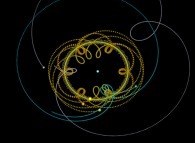
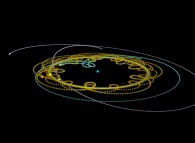
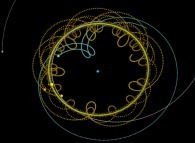
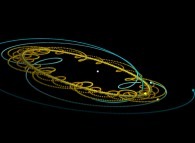
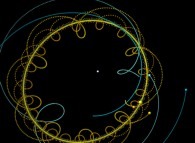
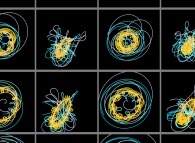
Au lieu d'utiliser un point fixe O (dans ce qui précède, ce point était dans la proche banlieue
du Soleil) pour visualiser les trajectoires, il est possible d'utiliser un point quelconque,
éventuellement mobile, et en particulier l'un des corps étudiés (supposé de numéro R).
Pour le corps de numéro k,
l'ensemble des points à représenter devient :
-------> -------> ----------> ----------> ----------> ----------> ----------> ---------->
S' = {[ OC (0) - OC (0) ] , [ OC (1.dt) - OC (1.dt) ] , [ OC (2.dt) - OC (2.dt) ] ,..., [ OC (n.dt) - OC (n.dt) ] ,...}
k k R k R k R k R
Cette simple idée va nous permettre d'accéder à des visualisations originales
du système solaire comme cela va être montré par la suite...
