/*************************************************************************************************************************************/
/* */
/* D E F I N I T I O N D E L A N - B O U T E I L L E D E K L E I N */
/* D I T E " V E R S I O N 1 " N O N S I M P L I F I E E */
/* ( S U R F A C E U N I L A T E R E S I ' N ' E S T I M P A I R ) : */
/* */
/* */
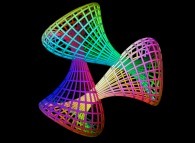
/* Definition de la surface (due a Patrice Jeener, 'v $xrs/bKlein.31$K') : */
/* */
/* Elle est definie parametriquement */
/* en fonction des deux parametres 'u' */
/* et 'v' : */
/* */
/* 8.S S+1 */
/* H(u,v) = -----.sin(-----.u) */
/* S+1 2 */
/* */
/* p ___ */
/* W(u,v) = cos((S+1).u + ---) + \/ 2 */
/* T */
/* */
/* DX(u,v) = -S.sin(u) - S.sin(S.u) */
/* */
/* DY(u,v) = +S.cos(u) - S.cos(S.u) */
/* */
/* W(u,v).DY */
/* F (u,v) = S.cos(u) + cos(S.u) - -----------.cos(v) */
/* x H */
/* */
/* W(u,v).DX */
/* F (u,v) = S.sin(u) - sin(S.u) - -----------.cos(v) */
/* y H */
/* */
/* F (u,v) = W(u,v).sin(v) */
/* z */
/* */
/* avec : */
/* */
/* u ∈ [ 0 , 2.p ] */
/* */
/* v ∈ [ 0 , 2.p ] */
/* */
/* (ou 'p' designe 'pi'). */
/* */
/* */
/* A titre d'exemple, voici quelques */
/* jeux de parametres {S,T} utiles : */
/* */
/* {S=2,T=4} ==> triple bouteille de Klein (N=3), */
/* {S=3,T=5} ==> quadruple "bouteille de Klein" (N=4), */
/* {S=4,T=6} ==> quintuple bouteille de Klein (N=5). */
/* */
/* Evidemment la surface obtenue n'est unilatere */
/* que si 'N' est impair. Ainsi, la "triple bouteille" */
/* est bien une bouteille de Klein, alors que la "quadruple */
/* bouteille" est une fausse bouteille de Klein car bilatere... */
/* */
/* */
/*************************************************************************************************************************************/
/*************************************************************************************************************************************/
/* */
/* D E F I N I T I O N D E L A N - B O U T E I L L E D E K L E I N */
/* D I T E " V E R S I O N 1 " S I M P L I F I E E */
/* ( S U R F A C E U N I L A T E R E S I ' N ' E S T I M P A I R ) : */
/* */
/* */
/* Definition (due a Patrice Jeener et simplifiee aux environs du 20030304171944 par Edmond Bonan, 'v $xrs/bKlein.51$K') : */
/* */
/* Elle est definie parametriquement */
/* en fonction des deux parametres 'u' */
/* et 'v' : */
/* */
/* S+1 p ___ */
/* W(u,v) = -----.(cos((S+1).u + ---) + \/ 2 ) */
/* 4 T */
/* */
/* S-1 */
/* F (u,v) = S.cos(u) + cos(S.u) - W(u,v).sin(-----.u).cos(v) */
/* x 2 */
/* */
/* S-1 */
/* F (u,v) = S.sin(u) - sin(S.u) - W(u,v).cos(-----.u).cos(v) */
/* y 2 */
/* */
/* F (u,v) = W(u,v).sin(v) */
/* z */
/* */
/* avec : */
/* */
/* u ∈ [ 0 , 2.p ] */
/* */
/* v ∈ [ 0 , 2.p ] */
/* */
/* (ou 'p' designe 'pi'). */
/* */
/* */
/* A titre d'exemple, voici quelques */
/* jeux de parametres {S,T} utiles : */
/* */
/* {S=2,T=4} ==> triple bouteille de Klein (N=3), */
/* {S=3,T=5} ==> quadruple "bouteille de Klein" (N=4), */
/* {S=4,T=6} ==> quintuple bouteille de Klein (N=5). */
/* */
/* Evidemment la surface obtenue n'est unilatere */
/* que si 'N' est impair. Ainsi, la "triple bouteille" */
/* est bien une bouteille de Klein, alors que la "quadruple */
/* bouteille" est une fausse bouteille de Klein car bilatere... */
/* */
/* */
/*************************************************************************************************************************************/