/*===================================================================================================================================*/
/*************************************************************************************************************************************/
/* */
/* D E F I N I T I O N D E S T R O I S F O N C T I O N S ' F ' : */
/* */
/* */
/* Definition de la surface ('v $xrs/huit.11$K') : */
/* */
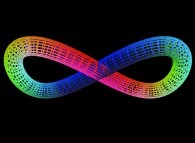
/* Le pseudo-tore a deux trous est defini parametriquement */
/* en fonction des deux parametres 'u' */
/* (appele aussi 'distance polaire' ou */
/* 'theta' ou encore 'latitude') et 'v' */
/* (appele aussi 'longitude' ou 'phi') : */
/* */
/* Choix(u,v) = +1 si v < M.(4.pi/D) */
/* = -1 sinon */
/* */
/* __________ */
/* / A+cos(v) */
/* XPlan(u,v) = R.Choix(u,v).\/ ---------- */
/* B */
/* */
/* sin(v) */
/* YPlan(u,v) = R.-------- */
/* C */
/* Definition d'une courbe plane en forme de "8". */
/* */
/* dXPlan(u,v) = d#XPlan(u,v) */
/* dYPlan(u,v) = d#YPlan(u,v) */
/* La tangente T est donc {+dXPlan(u,v),+dYPlan(u,v). */
/* */
/* Psi(u,v) = arctg(-dXPlan(u,v),+dYPlan(u,v)) */
/* La normale N est orthogonale a la tangente T */
/* et est donc {+dYPlan(u,v),-dXPlan(u,v)}. */
/* */
/* Xellipse(u,v) = Ra.cos(u) */
/* Yellipse(u,v) = 0 */
/* Zellipse(u,v) = Rb.sin(u) */
/* Definition d'une ellipse dans le plan {OX,OZ}. */
/* */
/* F (u,v) = [Xellipse(u,v)*cos(psi)] - [Yellipse(u,v)*sin(psi)] + XPlan(u,v) */
/* x */
/* */
/* F (u,v) = [Xellipse(u,v)*sin(psi)] + [Yellipse(u,v)*cos(psi)] + YPlan(u,v) */
/* y */
/* */
/* F (u,v) = Zellipse(u,v) */
/* z */
/* Definition d'une ellipse dont le centre est le point */
/* courant {XPlan(u,v),YPlan(u,v),0} et situee dans le */
/* plan {N,OZ}. */
/* */
/* et (parametres par defaut) : */
/* */
/* M=1 */
/* D=2 */
/* R=1 */
/* A=1 */
/* B=2 */
/* C=2 */
/* */
/* avec : */
/* */
/* u ∈ [ 0 , 2.p ] */
/* */
/* v ∈ [ 0 , 4.p ] */
/* */
/* (ou 'p' designe 'pi'). */
/* */
/* A cause de la derivee 'd#XPlan(u,v)' qui */
/* fait descendre 'A+cos(v)' en denominateur, */
/* il est imperatif que : */
/* */
/* A+cos(v) # 0 */
/* */
/* Si par malheur : */
/* */
/* A+cos(v) = 0 */
/* */
/* il convient d'ajouter un 'epsilon' a 'v' */
/* afin de supprimer cette nullite, d'ou la */
/* fonction 'v_corrige(v)' qui remplacera 'v' */
/* dans les definitions de 'Fx(u,v)' et de */
/* 'Fy(u,v)'. */
/* */
/* Ainsi, la coordonnee 'u' decrit la petite */
/* ellipse (de "rayons" 'Ra' et 'Rb') et 'v' */
/* decrit la courbe en forme de '8'. */
/* */
/* Tout ceci est tres inspire de 'v $xtc/huit.03$c' */
/* en faisant : */
/* */
/* u = phi ∈ [0,2.p] */
/* v = theta ∈ [0,4.p] */
/* */
/* */
/*************************************************************************************************************************************/