Kepler, Von Neumann and God

[More Rounding-off Error Visualizations]






Jean-François COLONNA
[Contact me]

www.lactamme.polytechnique.fr

CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 10/21/1996 and last updated on 10/03/2024 17:08:55 -CEST-)



(published in The Visual Computer, Volume 12, Number 7, 08/1996)


Abstract: Today, both fundamental and applied research rely heavily on computers. It is recalled that the numerical study of non linear models by means of these machines depends on programs, for the associative property of the multiplicative operator is lost. The N-body problem is used to display the sensitivity to numerical accuracy.


Keywords: numerical simulation, sensitivity to initial conditions, sensitivity to numerical accuracy, rounding-off errors, scientific visualization.



For chaotic processes, the sensivity to initial conditions is a well known phenomenon which is said to be the cause of the impossibility of long term forecast. In my point of view, there is a phenomenon of greater importance: the sensivity to numerical accuracy as already described in [01][02]. The rounding-off errors are inherent to the computer architecture and if for daily use 32 or 64 bit accuracy is enough, fixed-size accuracy will not be sufficient when running non linear programs. Moreover in this context the associative property of the multiplicative operator is lost and unfortunately, for most values A, B and C: 
                    (AxB)xC # Ax(BxC)
(this is also true for the addition, but the effect on the multiplication is worse). Let's recall this can be shown very easily with the Verhulst dynamics that models the variation of a population of individuals by the following iteration: 
                                       2
                    X  = (R+1)X    - RX
                     n         n-1     n-1
('R' denotes the growing rate. When R > 2.57 this shows a so-called "chaotic" behaviour.) A very simple short C program in double precision can be written in order to compute Xn for any value of n; unfortunately there are many ways to get the results as shown in the following two tables obtained on an IBM ES9000 and an IBM RS6000 (with R = 3.0): 
                    IBM ES9000:

                              (R+1)X-R(XX)   (R+1)X-(RX)X   ((R+1)-(RX))X  RX+(1-(RX))X   X+R(X-(XX))

                    X(00)   = 0.500000       0.500000       0.500000       0.500000       0.500000
                    X(10)   = 0.384631       0.384631       0.384631       0.384631       0.384631
                    X(20)   = 0.418895       0.418895       0.418895       0.418895       0.418895
                    X(30)   = 0.046399       0.046399       0.046399       0.046399       0.046399
                    X(40)   = 0.320185       0.320183       0.320188       0.320182       0.320189
                    X(50)   = 0.063406       0.064521       0.061895       0.064941       0.061244
                    X(60)   = 1.040381       0.846041       0.529794       1.319900       1.214070
                    X(70)   = 0.004104       1.199452       0.873553       0.573637       0.000009
                    X(80)   = 0.108044       0.121414       1.260726       0.395871       0.280590
                    X(90)   = 0.096374       0.089244       0.582157       0.344503       1.023735



                    IBM RS6000:

                              (R+1)X-R(XX)   (R+1)X-(RX)X   ((R+1)-(RX))X  RX+(1-(RX))X   X+R(X-(XX))

                    X(00)   = 0.500000       0.500000       0.500000       0.500000       0.500000
                    X(10)   = 0.384631       0.384631       0.384631       0.384631       0.384631
                    X(20)   = 0.418895       0.418895       0.418895       0.418895       0.418895
                    X(30)   = 0.046399       0.046399       0.046399       0.046399       0.046399
                    X(40)   = 0.320177       0.320184       0.320188       0.320190       0.320189
                    X(50)   = 0.067567       0.063747       0.061859       0.060822       0.061486
                    X(60)   = 0.001145       0.271115       0.616781       0.298613       1.307350
                    X(70)   = 1.296775       1.328462       0.486629       0.938605       1.054669
                    X(80)   = 0.553038       0.817163       1.277151       1.325437       0.617058
                    X(90)   = 0.094852       0.154184       1.174162       0.148151       0.237355


The consequence is that the results obtained may depend on many extra-parameters:

For example, maybe only a handful of readers will be able to reproduce exactly the preceding results since I did not give them neither the releases of the systems used nor the compiling options... Then, the user could be faced with impossibilities: for example, to reproduce results obtained before upgrading his or her computer. Moreover, the user can do nonsensical things, like, for example using simultaneously two or more non compatible computers for studying a non linear problem ; this case is visualized in [01] where the Lorenz attractor is computed in a parallel manner on two "identical" Silicon Graphics workstations, but unfortunately for two different system releases.

It is noteworthy to recall that the infinite Real number field is mapped on many different finite floating point number sets and that these sets are not themselves fields. One of the consequences is that one cannot study stricto sensu problems depending "heavily" on Real numbers (in the mathematical sense) with a computer: digital Real numbers do not exist! Today, where both fundamental and applied research rely heavily on computers [03], and where numerical techniques and devices are omnipresent, it is more than essential to recall to computer users those problems. To do so, I have chosen to exhibit the N-body problem. It is important for the reader to remember that my purpose here is not to talk about neither deterministic chaos, nor celestial mechanics, nor applied mathematics (this problem involving numerical integration methods); my only purpose here is only to show how dangerous it could be to do multiplications with a computer...

The N-body problem is the following one: N gravitationally interacting bodies are specified with their initial conditions (at time t=0) and we should like to know their individual positions at any time t. Since Kepler [04] and Newton [05] it is known that for N=2 the trajectories are elliptic. Unfortunately, as stated by Henri Poincare [06], for N strictly greater than 2, this problem cannot be studied analytically. Fortunately, in the forties, John Von Neumann and many others gave us the computer that can be used today to study anything... The N-body problem can then be numerically studied using the Newton law: 
                    -->    ------>
                     F = m. Gamma
for each of the studied body (k): 
                    --->     ------->
                     F  = m . Gamma
                      k    k      k
with: 
                                2 ---->
                               d   OC
                    ------->         k
                     Gamma  = ---------
                          k        2
                                 dt
and: 
                    
                      2 ---->    i=N
                     d   OC     -----       M
                           k    \            i     ----->
                    --------- = /     G ----------- C C
                         2      -----            3   k i
                       dt        i=1     |----->|
                                (i#k)    | C C  |
                                            k i
(where O and Ck denote respectively the origin of the coordinate system and the position of the number k body). Then, it "suffices" to solve a second order differential equation system in order to compute the instaneous coordinates of each bodies studied. I wrote such a program; the following inputs are needed for each body Ck:

(all values are given in the MKSA unit system).

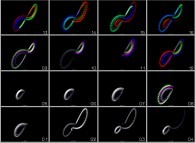
Figure displays the case where there are only two bodies (N=2). As expected the trajectory of the second one is an ellipse whose focus is the first one (chosen to be still). Figure displays our actual Solar System whose evolution is computed for about 18 years; its shows non chaotical trajectories (each of them are very close to an ellipse whose focus is the sun). Figure exhibits a very interesting case with four bodies (N=4); as a matter of fact a very heavy one (five times heavier than Jupiter) is located near the Sun in order to induce strong perturbations of the trajectories of the two light bodies. In this case, their trajectories are far from being elliptic or even periodic. Finally the same double precision C program with exactly the same initial conditions is run on three "compatible" computers:

As exhibited on figure and as expected, the three computers give us the same values resulting in white bodies (due to the superposition of the Red, the Green and the Blue colors). Unfortunately this does not last long. Slowly and then faster and faster, the predictions of the three computers become absolutely different; for example, the Red computer forecasts an ejection of the third body, when this last one seems to stay in orbit for the two other computers. So, where are the differences between the three machines? The major one lies in the compiler used; as a matter of fact, the three compilers do not translate the C statements into assembly instructions in the same way; then the loss of the associative property of the multiplication does the job!


Picture synthesis allows us to watch this phenomenon in a very dramatic way. The N-body problem is no exception; all non linear models I have numerically studied exhibit the same behaviour (please, see [01] where many examples are available as mpeg animations). So, what can be done ? To change the numerical method used to solve differential equations is of no help (by the way and paradoxically in these circumstances, higher order methods could be less efficient since they make use of a higher number of multiplications); anyway, the real problem lies at a lower level (the arithmetic used). To increase the accuracy of computers (going from to 64-bits to 128-bits or more), which is far from being economical, due to the nature of the problem, will just shift it some time steps later (after all, accuracy should be a function of speed...). As described in [01][02], I am suggesting a method to help telling which models are subject to this phenomenon. I should like to encourage reader involvement; in classroom settings students must be informed of this problem. Research must be conducted at all levels (hardware and software) to help preventing and solving it (if possible...). Finally a major question will remain unanswered maybe forever: which computer does God use to do the huge amount of computations needed to run our Universe in real time?






Copyright © Jean-François COLONNA, 1996-2024.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 1996-2024.