
A tridimensional pseudo-random walk defined by means of the Champernowne number -using all prime numbers-: 0.2 3 5 7 11 13 17 19 23 29 31... -168.982 digits, base 10- into 122525... -217.156 digits, base 6- [Une pseudo-marche aléatoire tridimensionnelle définie à l'aide du nombre de Champernowne -utilisant tous les nombres premiers-: 0.2 3 5 7 11 13 17 19 23 29 31... -168.982 chiffres, base 10- converti en 122525... -217.156 chiffres, base 6-].
Each digit N -base 6- defines the current step of an "absolute" tridimensional random walk:
digit=0 ==> move(+1,0,0)
digit=1 ==> move(-1,0,0)
digit=2 ==> move(0,+1,0)
digit=3 ==> move(0,-1,0)
digit=4 ==> move(0,0,+1)
digit=5 ==> move(0,0,-1)
The coordinates {X,Y,Z} are renormalized as follows:
[+0.3339,+0.6920]x[+0.4644,+1.1134]x[-0.0931,+0.3148] --> [0.1,0.9]x[0.1,0.9]x[0.1,0.9]
See some famous real numbers (possibly including this one):
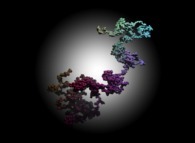
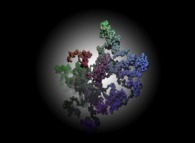
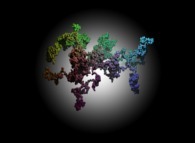
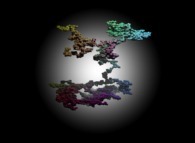
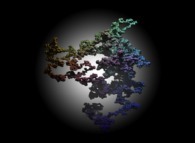
See a random number:

See a tridimensional brownian motion:
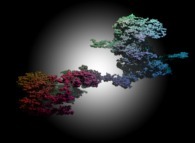
(CMAP28 WWW site: this page was created on 03/07/2019 and last updated on 09/05/2024 14:15:52 -CEST-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2019-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2019-2024.







