/*===================================================================================================================================*/
/*************************************************************************************************************************************/
/* */
/* D E F I N I T I O N D E S T R O I S F O N C T I O N S ' F ' : */
/* */
/* */
/* Definition de la surface ('v $xrs/epicycloide.31$K') : */
/* */
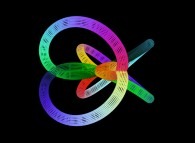
/* Le pseudo-tore "epicycloidal tridimensionnel" */
/* est defini parametriquement */
/* en fonction des deux parametres 'u' */
/* (appele aussi 'distance polaire' ou */
/* 'theta' ou encore 'latitude') et 'v' */
/* (appele aussi 'longitude' ou 'phi') : */
/* */
/* EX.v ECX ESX */
/* XEspace(u,v) = KX.e .[cos (OCX.v+PCX).sin (OSX.v+PSX)] + TX */
/* */
/* EY.v ECY ESY */
/* YEspace(u,v) = KY.e .[cos (OCY.v+PCY).sin (OSY.v+PSY)] + TY */
/* */
/* EZ.v ECZ ESZ */
/* ZEspace(u,v) = KZ.e .[cos (OCZ.v+PCZ).sin (OSZ.v+PSZ)] + TZ */
/* Courbe "epicycloidale tridimensionnelle". */
/* */
/* dXEspace(u,v) = d#XEspace(u,v) */
/* dYEspace(u,v) = d#YEspace(u,v) */
/* dZEspace(u,v) = d#ZEspace(u,v) */
/* */
/* Le vecteur {dXEspace(u,v),dYEspace(u,v),dZEspace(u,v)} defini un nouveau */
/* referentiel {{X1,X2,X3},{Y1,Y2,Y3},{Z1,Z2,Z3}} */
/* */
/* Xellipse(u,v) = Ra.cos(u) */
/* Yellipse(u,v) = Rb.sin(u) */
/* Zellipse(u,v) = 0 */
/* Definition d'une ellipse dans le plan {OX,OY}. */
/* */
/* F (u,v) = [Xellipse(u,v)*X1] + [Yellipse(u,v)*Y1] + [Zellipse(u,v)*Z1] + XEspace(u,v) */
/* x */
/* */
/* F (u,v) = [Xellipse(u,v)*X2] + [Yellipse(u,v)*Y2] + [Zellipse(u,v)*Z2] + YEspace(u,v) */
/* y */
/* */
/* F (u,v) = [Xellipse(u,v)*X3] + [Yellipse(u,v)*Y3] + [Zellipse(u,v)*Z3] + ZEspace(u,v) */
/* z */
/* Definition d'une ellipse dont le centre est le point */
/* courant {XEspace(u,v),YEspace(u,v),ZEspace(u,v)} et */
/* situee dans {Alpha(u,v),Beta_(u,v),Gamma(u,v)}. */
/* */
/* et (parametres par defaut) : */
/* */
/* KX = +1 */
/* TX = 0 */
/* EX = 0 */
/* ECX = +1 */
/* ESX = 0 */
/* OCX = +1 */
/* OSX = +1 */
/* PCX = 0 */
/* PSX = 0 */
/* */
/* KY = +1 */
/* TY = 0 */
/* EY = 0 */
/* ECY = +1 */
/* ESY = +1 */
/* OCY = +1 */
/* OSY = +1 */
/* PCY = 0 */
/* PSY = 0 */
/* */
/* KZ = +1 */
/* TZ = 0 */
/* EZ = 0 */
/* ECZ = 0 */
/* ESZ = +1 */
/* OCZ = +1 */
/* OSZ = +1 */
/* PCZ = 0 */
/* PSZ = 0 */
/* */
/* avec : */
/* */
/* u ∈ [ 0 , 2.p ] */
/* */
/* v ∈ [ 0 , 2.p ] */
/* */
/* (ou 'p' designe 'pi'). */
/* */
/* Tout ceci est tres inspire de 'v $xrk/SinCos.11$K' */
/* en faisant : */
/* */
/* v = t */
/* */
/* */
/*************************************************************************************************************************************/