/*************************************************************************************************************************************/
/* */
/* D E F I N I T I O N D E S N O M B R E S P S E U D O - H Y P E R - C O M P L E X E S */
/* ( O U " P S E U D O - Q U A T E R N I O N S " ) : */
/* */
/* */
/* Definition : */
/* */
/* Les nombres complexes peuvent etre representes */
/* de deux facons differentes comme couple de nombres */
/* reels : {x,y} en coordonnees cartesiennes et {rho,theta} */
/* en coordonnees polaires. */
/* */
/* L'addition de deux nombres complexes 'z1' et 'Z2' */
/* est facile a exprimer en coordonnees cartesiennes : */
/* */
/* z = z + z = (x ,y ) + (x ,y ) */
/* 1 2 1 1 2 2 */
/* */
/* = (x + x ,y + y ) */
/* 1 2 1 2 */
/* */
/* alors que la multiplication est plus facile a exprimer */
/* en coordonnees polaires : */
/* */
/* z = z . z = (rho ,theta ) . (rho ,theta ) */
/* 1 2 1 1 2 2 */
/* */
/* = (rho . rho ,theta + theta ) */
/* 1 2 1 2 */
/* */
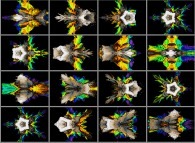
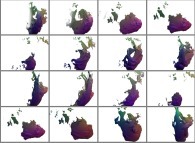
/* Les pseudo-nombres baptises "pseudo-hyper-complexes" */
/* (ou "pseudo-quaternions") seront representes de deux */
/* facons differentes comme quadruplets de nombres reels : */
/* {x,y,z,t} en coordonnees cartesiennes et {rho,theta,phi,alpha} */
/* en coordonnees hyper-spheriques. */
/* */
/* L'addition de deux "pseudo-quaternions" 'q1' et 'q2' */
/* sera definie en coordonnees cartesiennes par : */
/* */
/* q = q + q = (x ,y ,z ,t ) + (x ,y ,z ,t ) */
/* 1 2 1 1 1 1 2 2 2 2 */
/* */
/* = (x + x ,y + y ,z + z ,t + t ) */
/* 1 2 1 2 1 2 1 2 */
/* */
/* alors que seront utilisees les coordonnees hyper-spheriques */
/* pour definir la multiplication : */
/* */
/* q = q . q = (rho ,theta ,phi ,alpha ) . (rho ,theta ,phi ,alpha ) */
/* 1 2 1 1 1 1 2 2 2 2 */
/* */
/* = (rho . rho ,theta + theta ,phi + phi ,alpha + alpha ) */
/* 1 2 1 2 1 2 1 2 */
/* */
/* Par soucis de generalite, les combinaisons entre les quatre */
/* composantes {rho,theta,phi,alpha} des deux "pseudo-quaternions" */
/* seront en fait effectuees via des polynomes 'P' du quatrieme */
/* degre a deux variables initialises par defaut de facon a ce que : */
/* */
/* P(rho ,rho ) = rho . rho */
/* 1 2 1 2 */
/* */
/* P(theta ,theta ) = theta + theta */
/* 1 2 1 2 */
/* */
/* P(phi ,phi ) = phi + phi */
/* 1 2 1 2 */
/* */
/* P(alpha ,alpha ) = alpha + alpha */
/* 1 2 1 2 */
/* */
/* */
/*************************************************************************************************************************************/