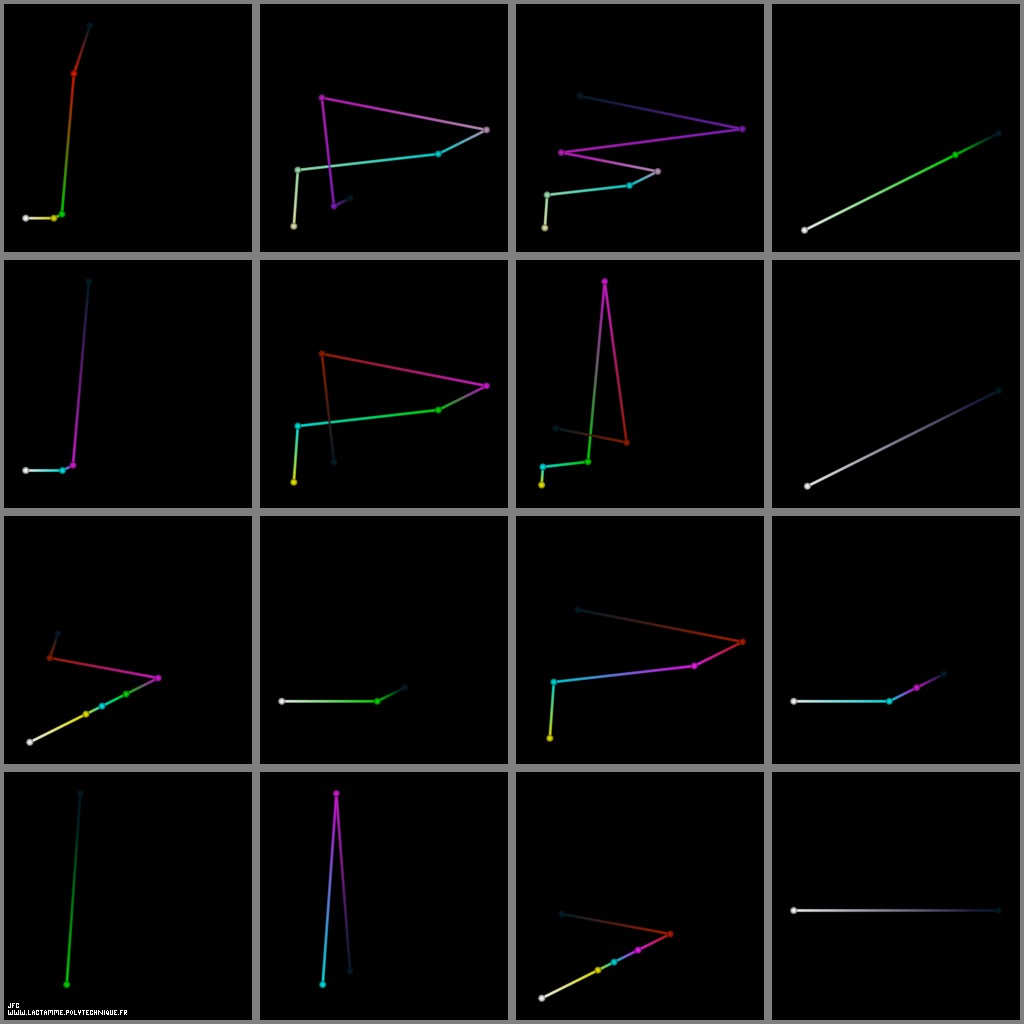
The Syracuse Conjecture for U(0)={5,6,7,8,...,20} -tridimensional display- [La conjecture de Syracuse pour U(0)={5,6,7,8,...,20} -visualisation tridimensionnelle-].

The Syracuse Conjecture for U(0)={5,6,7,8,...,20} -tridimensional display- [La conjecture de Syracuse pour U(0)={5,6,7,8,...,20} -visualisation tridimensionnelle-].
U = N (an integer number [un nombre entier]) > 0
0
if U is even [si U est pair] :
n n
U
n
U = ----
n+1 2
else [sinon] :
U = 3*U + 1
n+1 n
U(0) = 7
U(1) = 22
U(2) = 11
U(3) = 34
U(4) = 17
U(5) = 52
U(6) = 26
U(7) = 13
U(8) = 40
U(9) = 20
U(10) = 10
U(11) = 5
U(12) = 16
U(13) = 8
U(14) = 4
U(15) = 2
U(16) = 1
X coordinates = {U(0),U(3),U(6),...}
Y coordinates = {U(1),U(4),U(7),...}
Z coordinates = {U(2),U(5),U(8),...}
with a renormalization inside [0,1] for the three sets of coordinates.
The colors used are a function of 'n' (from Dark Blue [n=0] to White with an increasing luminance  ).
).