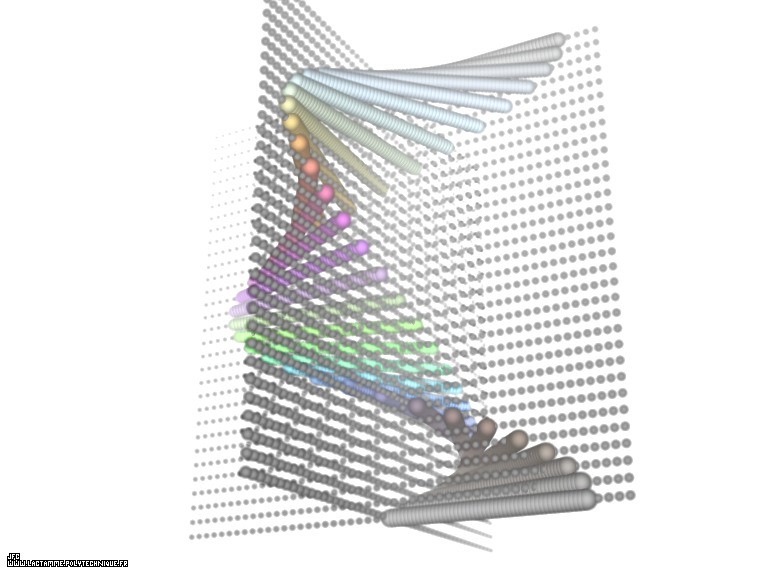
32 points on a trigonometric circle [32 points sur un cercle trigonométrique].

32 points on a trigonometric circle [32 points sur un cercle trigonométrique].
X(3) + + X(2)
+ +
+ +
+ # C(2)
+ + */*
+ + *///*
+ + */////*
+ + *///////*
+ + */////////*
+ + *///////////
- - - - - - - - - - - - - - - O + + + + + + +/+/+/+/+/+/# + + X(1)
- - */////////C(1)
- - */////////*
- - *///////*
- - */////*
- - *///*
- - */*
- # C(3)
- -
- -
- -
assuming that:
C(1) > 0
C(2) > 0
C(3) < 0