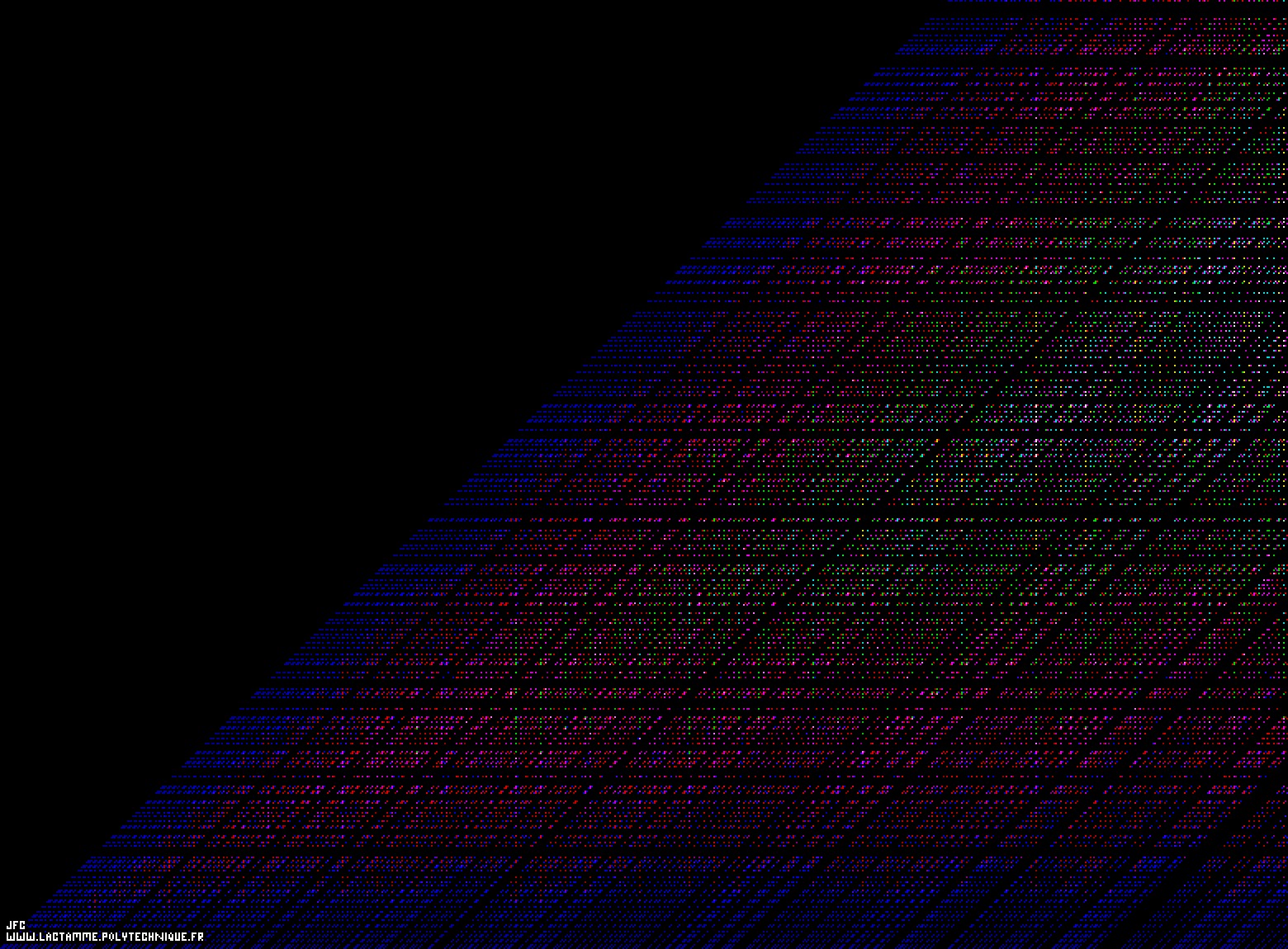
The Goldbach conjecture for the even numbers from 6 to 1564 [La conjecture de Goldbach pour les entiers pairs de 6 à 1564].




The Goldbach conjecture states that each even integer number N greater or equal to 4 can be written as the sum of two prime numbers. For example: 
                    4   = 2+2
                    6   = 3+3
                    8   = 3+5 [= 5+3]
                    10  = 3+7 = 5+5 [= 7+3]
                    (...)
                    990 =   7+983 =  13+977 =  19+971 =  23+967 =  37+953 =  43+947 =  53+937 =  61+929 =  71+919 =  79+911
                        =  83+907 = 103+887 = 107+883 = 109+881 = 113+877 = 127+863 = 131+859 = 137+853 = 151+839 = 163+827
                        = 167+823 = 179+811 = 181+809 = 193+797 = 229+761 = 233+757 = 239+751 = 251+739 = 257+733 = 263+727
                        = 271+719 = 281+709 = 307+683 = 313+677 = 317+673 = 331+659 = 337+653 = 347+643 = 349+641 = 359+631
                        = 373+617 = 383+607 = 389+601 = 397+593 = 419+571 = 421+569 = 433+557 = 443+547 = 449+541 = 467+523
                        = 487+503 = 491+499
                       [= 499+491 = 503+487 = 523+467 = 541+449 = 547+443 = 557+433 = 569+421 = 571+419 = 593+397 = 601+389
                        = 607+383 = 617+373 = 631+359 = 641+349 = 643+347 = 653+337 = 659+331 = 673+317 = 677+313 = 683+307
                        = 709+281 = 719+271 = 727+263 = 733+257 = 739+251 = 751+239 = 757+233 = 761+229 = 797+193 = 809+181
                        = 811+179 = 823+167 = 827+163 = 839+151 = 853+137 = 859+131 = 863+127 = 877+113 = 881+109 = 883+107
                        = 887+103 = 907+83  = 911+79  = 919+71  = 929+61  = 937+53  = 947+43  = 953+37  = 967+23  = 971+19
                        = 977+13  = 983+7]
                    (...)


The vertical axis represents the odd numbers P={3, 5, 7, 9,...} starting at 3 (and then includes the prime numbers excluding the first one -2- that is even), when the horizontal axis represents the even numbers N={6, 8, 10, 12,...} starting at 6 (this process does not start at 4=2+2 in order to avoid the first prime number -2 that is an even number- on the vertical axis). Each N-vertical line exhibits the decompositions of N as sums of two prime numbers (N=P1+P2, P1 and P2 having the same color).


See some related visualizations (including this one):

 
 
 
 



(CMAP28 WWW site: this page was created on 01/11/2013 and last updated on 10/20/2022 12:46:39 -CEST-)



[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François Colonna, 2013-2022.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / Ecole Polytechnique, 2013-2022.