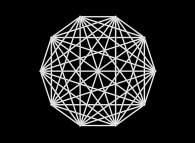
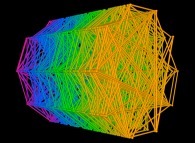
The 1.000 first digits -base 10- of 'e' displayed on an helix -good point of view- [Les 1.000 premières décimales -base 10- de 'e' visualisées sur une hélice -bon point de vue-].
The 1.000 first digits -base 10- of 'e' displayed on an helix -good point of view- [Les 1.000 premières décimales -base 10- de 'e' visualisées sur une hélice -bon point de vue-].
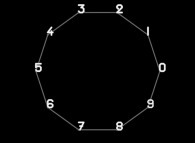To each digit D inside [0,9] is associated an angle A(D) with the following rule:
A(D) = D.(2.pi/10)Then each digit D(n) (n ∈ [1,1000] for this picture) is displayed as a point (belonging to an helix) with the following tridimensional coordinates:
X = cos(A(D(n)))
Y = sin(A(D(n)))
Z = n
At last, the picture displays all the segments {D(n),D(n+1)} (for all n).
