The Ulam Spiral and its generalizations
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 04/25/2012 and last updated on 10/03/2024 17:20:12 -CEST-)
[en français/in french]
Abstract: What is the Ulam Spiral and how can it be extended?
Keywords: Ulam Spiral, Spirale d'Ulam, Prime Numbers, Nombres Premiers.
Contents of this page:
1-DEFINITION OF THE ULAM SPIRAL:
In 1963 the mathematician Stanislas Ulam had the idea to draw a "square spiral" on a squared sheet of paper.
Starting from the center, he numbered (N=1, 2, 3, 4,...) each of its integer points encountered as follows:
5----4----3
| | .
| | .
6 1----2 .
| |
| |
7----8----9----10
and then he marked ("X") each point whose number N was a prime number (2, 3, 5, 7,...):
X----4----X
| | .
| | .
6 1----X .
| |
| |
X----8----9----10
(1 being not a prime number). This process can be programmed in a computer; it gives birth to numerous pictures and for example the following one
that displays 2025 numbers (including 306 prime numbers):

where the green square denotes 1 and the white ones the prime numbers.
This picture exhibits the fact that prime numbers are not distributed randomly for some bidimensional patterns appear.
The structures reveal us polynoms of the second degree and for example the Euler formula:
2
f(n) = n - n + 41
n ∈ [1,40]
that gives prime numbers for all values of n between 1 and 40.
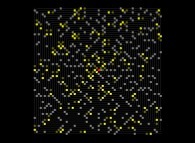
It is interesting to compare the Ulam spiral to a random picture with the same percentage (15%) of white squares:

Here are four pictures displaying the 'P-twin' prime numbers (set of two prime numbers {P1,P2}
such that on the one hand P2-P1=P [P being an even number] and that on the other hand there are no prime number between P1 and P2):



2-SOME GENERALIZATIONS:
In the 1980's, I had the idea to generalize this process displaying ND (the number of divisors of N;
let's recall that prime numbers have only two divisors: 1 and themselves).
Hence the following picture displaying 2025 numbers:

where the green square denotes 1 and the white ones the prime numbers,
when the red squares display the other numbers, their luminance being
porportionnal to ND.
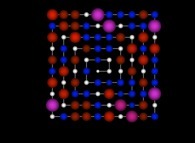
The two following pictures display respectively 100 and 1000 numbers by means of a different visualization
code. ND is shown simutaneously using the radius of each sphere as well as the increasing luminance
of colors:

Moreover, there are many other ways to exhibit these informations. For example, ND
can be displayed using a third dimension:

Obviously other types of spirals can be used and for example the Archimedes one:

At last, the following pictures are displaying the so-called smoothess of the integers.
An integer N is said to be K-smooth if it does not have prime factors greater than K.
Each integer N is visualized using a sphere whose luminance and radius are decreasing functions of log(K):



3-ULAM SPIRAL AND ARTISTIC CREATION:
The Ulam spiral and the prime numbers can be a source of artistic inspiration as exhibited with the following pictures:



by means of various processes: conformal transformations, filtering, extended life game,...
that allow deformations, transformations, smoothings,... of the Ulam spiral and of some of its generalizations.
Copyright © Jean-François COLONNA, 2012-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2012-2024.















