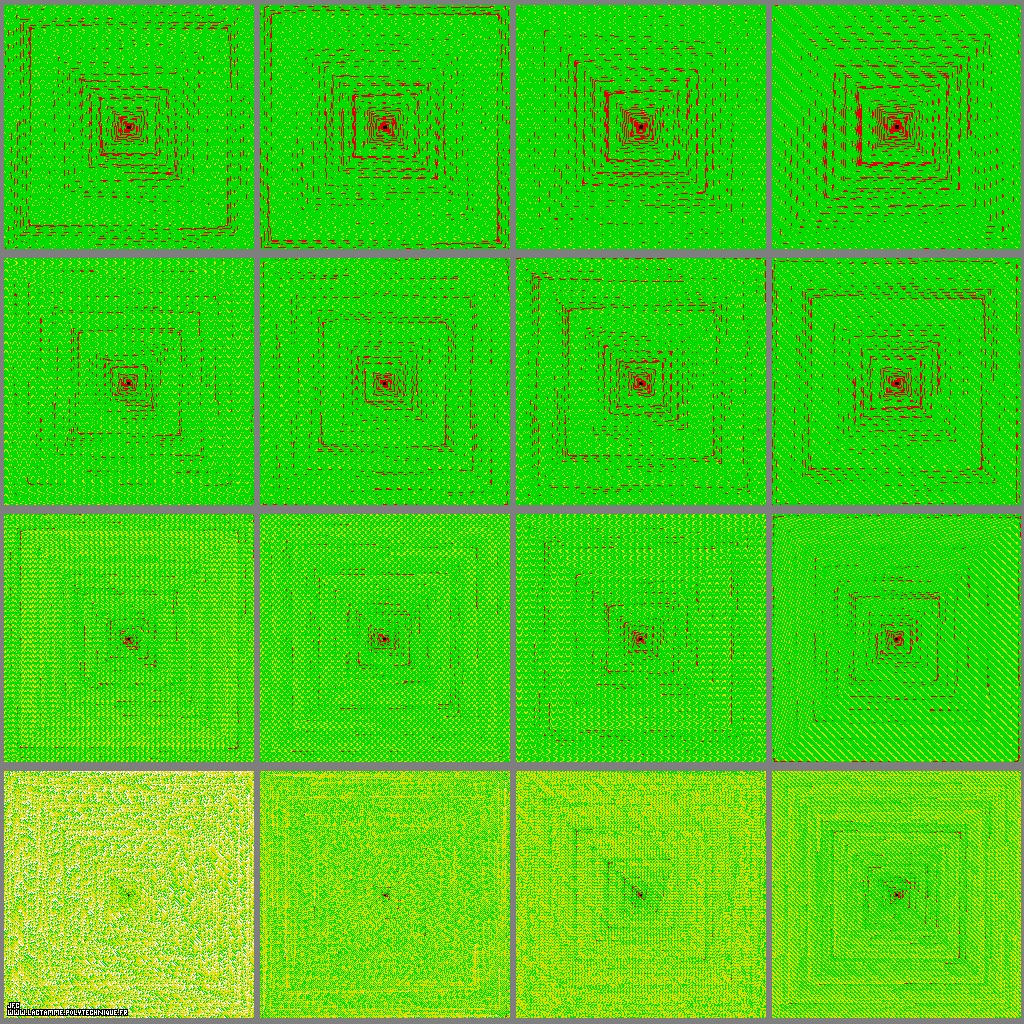
The additive persistence of the 65536 first integer numbers for the bases 2 -lower left- to 17 -upper right- [La persistance additive des 65536 premiers nombres entiers pour les bases 2 -en bas et à gauche- à 17 -en haut et à droite-].

The additive persistence of the 65536 first integer numbers for the bases 2 -lower left- to 17 -upper right- [La persistance additive des 65536 premiers nombres entiers pour les bases 2 -en bas et à gauche- à 17 -en haut et à droite-].
5----4----3
| | .
| | .
6 1----2 .
| |
| |
7----8----9----10
PA(N,B) = the additive persistence of N for the base B,
f(...) = an arbitrary ascending function
Let's define PA(N,B) with an obvious example:
B = 10
2 1 0
N = 856 (= 8xB + 5xB + 6xB )
Then the following sequence is computed:
856 ---> (8+5+6) = 19 ---> (1+9) = 10 ---> (1+0) = 1
1 2 3
PA(856,10) = 3


