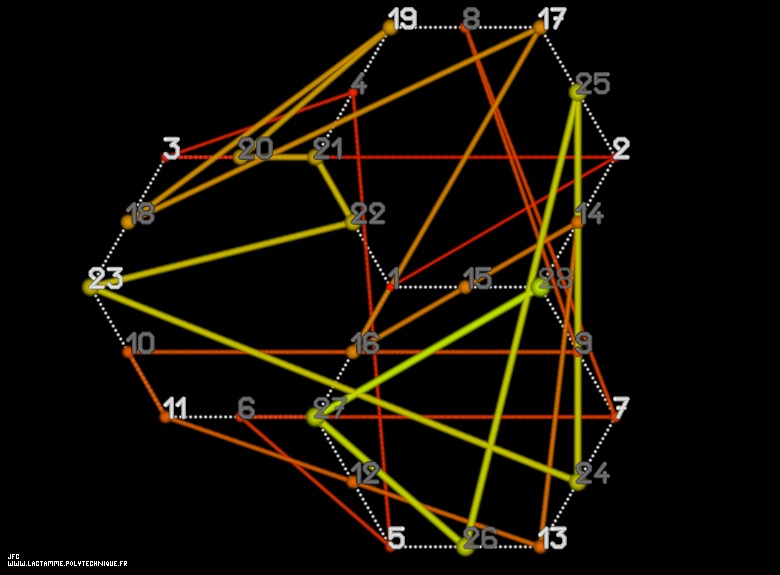
AVirtualMachineForExploringSpaceTimeAndBeyond : Three hexagons and the twenty-eight first strictly positive integer numbers -nine of them being prime numbers- (Trois hexagones et les vingt-huit premiers nombres entiers strictement positifs -neuf d'entre-eux etant des nombres premiers-).

Three hexagons and the twenty-eight first strictly positive integer numbers -nine of them being prime numbers- [Trois hexagones et les vingt-huit premiers nombres entiers strictement positifs -neuf d'entre-eux étant des nombres premiers-].

A structure (white dotted lines) is built using three contiguous hexagons. This structure has V=3*6-((3*1)+(1*2))=13 different vertices and S=(3*6)-(3*1)=15 different sides. The N=V+S=13+15=28 first strictly positive integer numbers {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28} are located on this structure with the following constraints:

The P=9 first prime numbers {2,3,5,7,11,13,17,19,23}, recalling that 1 is not a prime number, are on "special" vertices (white figures), when the N-P=28-9=19 remaining integer numbers are on the remaining vertices as well as on the middle of each side (grey figures). Then each of the N integer numbers is used once and only once.

All the sums of the three different numbers contained on each side (two on the vertices and one on the middle) must be equal to a certain value (a priori unknown):

                    
                     1 + 15 + 28 = 44
                     1 + 16 + 27 = 44
                     1 + 21 + 22 = 44
                     2 + 14 + 28 = 44
                     2 + 17 + 25 = 44
                     3 + 18 + 23 = 44
                     3 + 20 + 21 = 44
                     4 + 19 + 21 = 44
                     5 + 12 + 27 = 44
                     5 + 13 + 26 = 44
                     6 + 11 + 27 = 44
                     7 +  9 + 28 = 44
                     7 + 13 + 24 = 44
                     8 + 17 + 19 = 44
                    10 + 11 + 23 = 44

The colored lines (starting with 1 -red, at the center of the structure- and ending with 28 -yellow, in the middle right-) display the natural order of the integer numbers.

[See the C program used to solve the problem]

(CMAP28 WWW site: this page was created on 02/28/2013 and last updated on 01/23/2023 18:54:27 -CET-)

[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]

Copyright © Jean-François Colonna, 2013-2023. Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2013-2023.

Copyright © Jean-François Colonna, 2013-2023.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2013-2023.