The staging of numbers
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 08/06/2015 and last updated on 01/27/2025 13:47:12 -CET-)
[en français/in french]
To make progress in our knowledge of the Universe, we must
do Mathematics: juggling with formulas, solving equations,...
All this is generally abstract, but nothing forbids us to use
the sense that evolution has given us and particularly the vision;
our eyes are made to be surprised, and today the computer
allows us a new experimental approach: the virtuality.
A so-called virtual experiment 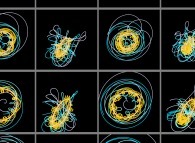 will consist of the in silico
study of a model of a certain system (elementary particles
will consist of the in silico
study of a model of a certain system (elementary particles 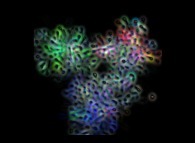 to the Universe
to the Universe  ).
After very heavy computations, raw results are mountains
of numerical values that are a priori useless without further
processing, a "staging".
And this is true regarding the real experiments: telescopes or again particle accelerators
generate very very huge quantities of measures that have to be exploited.
).
After very heavy computations, raw results are mountains
of numerical values that are a priori useless without further
processing, a "staging".
And this is true regarding the real experiments: telescopes or again particle accelerators
generate very very huge quantities of measures that have to be exploited.
THen what to do with all these numbers? Obviously reading them would be a non sense.
Is there an objective way to exhibit them? Their display as pictures seems
to be the best solution: as a matter of fact our visual system is a high
bandwidth processor that can instantaneously react to surprises. This translation
of numbers into pictures implies the existence of an universal code.
But is it true?
On the one hand almost all our display systems (sheet of paper, screens,...) are
bidimensional. When displaying sets of dimension 3 and higher, projections will be
mandatory thus hidden their full complexity. But we are accustomed with this process for
it is the case with protography. No problem with familiar objects: everybody has seen
mountains (fractal ones...)  ,
but with unfamiliar objects like this unkonwn structure
,
but with unfamiliar objects like this unkonwn structure  its understanding is more difficult. Beyond the third dimension, the situation will worsen
and rotations or again cross-sections will be used as with this Julia set
its understanding is more difficult. Beyond the third dimension, the situation will worsen
and rotations or again cross-sections will be used as with this Julia set  computed in a 8 dimensions space.
computed in a 8 dimensions space.
On the other hand many measures (real or virtual ones) do not have pictures at all (a pressure
field for example). Moreover, pictures could be sometimes forbidden:
this is the case with the Quantum Mechanics that does not allow this picture
of a nucleon  since positions,
velocities, shapes or again colors have no meaning there.
since positions,
velocities, shapes or again colors have no meaning there.
Nevertheless one could believe that with very simple sets, objective representations
could be devised. Let's recall that a numerical screen is a bidimensional array of
numerical values (colors and luminances). Then the display of a matrix should be objective.
Unfortunately, this example  shows it is false.
As a matter of fact to visualize this array one have to answer to stupid questions
like: "what is the color of 23?". Obviously the answer is arbitrary: in this picture four
different sets of colors are used and the four sub-pictures then obtained seem to exhibit
four different objects and worse, four incompatible objects (see the discontinuity and
the periodicity that appears and disapppears at will...). Then one can hide that exists and one
can exhibit that does not!
shows it is false.
As a matter of fact to visualize this array one have to answer to stupid questions
like: "what is the color of 23?". Obviously the answer is arbitrary: in this picture four
different sets of colors are used and the four sub-pictures then obtained seem to exhibit
four different objects and worse, four incompatible objects (see the discontinuity and
the periodicity that appears and disapppears at will...). Then one can hide that exists and one
can exhibit that does not!
Thus if the objective display of a bidimensional array is impossible, it is
obvious that the objective display of more complex sets is impossible...
At last it is useful to remember that these pictures are computed to be viewed
by people. Then one must not forget that our visual system is subject to optical
illusions. For example the one of simultaneous contrast  that exhibits the fact that it is impossible to compare the luminance of two distant points of a picture.
that exhibits the fact that it is impossible to compare the luminance of two distant points of a picture.
Then objectivity and unicity do not exist for the display of numerical sets. Nevertheless,
it is useful to devise some useful practical rules: to prefer simple pictures rather that complex ones,
to use the so-called cold and warm colors
for negative an positive values respectively,
to extend the notion of point of view including colors and shapes,
to add interactivity in order to change easily the points of view,
to specify explicitely the used codes,...
Beside these difficulties one must not forget the ones inherent to the use of computers:
programming is very difficult
or again the fact that numerical computations are not safe.
Nevertheless scientists and engineers have in their hands new tools that will be
as revolutionary as the microscope and the telescope in their times
and a wonderful opportunity for an encounter between Art and Science  .
.
Copyright © Jean-François COLONNA, 2015-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2015-2025.
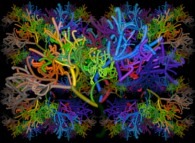
 will consist of the in silico
study of a model of a certain system (elementary particles
will consist of the in silico
study of a model of a certain system (elementary particles  to the Universe
to the Universe  ).
After very heavy computations, raw results are mountains
of numerical values that are a priori useless without further
processing, a "staging".
And this is true regarding the real experiments: telescopes or again particle accelerators
generate very very huge quantities of measures that have to be exploited.
).
After very heavy computations, raw results are mountains
of numerical values that are a priori useless without further
processing, a "staging".
And this is true regarding the real experiments: telescopes or again particle accelerators
generate very very huge quantities of measures that have to be exploited.
 ,
but with unfamiliar objects like this unkonwn structure
,
but with unfamiliar objects like this unkonwn structure  its understanding is more difficult. Beyond the third dimension, the situation will worsen
and rotations or again cross-sections will be used as with this Julia set
its understanding is more difficult. Beyond the third dimension, the situation will worsen
and rotations or again cross-sections will be used as with this Julia set  computed in a 8 dimensions space.
computed in a 8 dimensions space.
 shows it is false.
As a matter of fact to visualize this array one have to answer to stupid questions
like: "what is the color of 23?". Obviously the answer is arbitrary: in this picture four
different sets of colors are used and the four sub-pictures then obtained seem to exhibit
four different objects and worse, four incompatible objects (see the discontinuity and
the periodicity that appears and disapppears at will...). Then one can hide that exists and one
can exhibit that does not!
shows it is false.
As a matter of fact to visualize this array one have to answer to stupid questions
like: "what is the color of 23?". Obviously the answer is arbitrary: in this picture four
different sets of colors are used and the four sub-pictures then obtained seem to exhibit
four different objects and worse, four incompatible objects (see the discontinuity and
the periodicity that appears and disapppears at will...). Then one can hide that exists and one
can exhibit that does not!
 that exhibits the fact that it is impossible to compare the luminance of two distant points of a picture.
that exhibits the fact that it is impossible to compare the luminance of two distant points of a picture.
 .
.